Talsystem
Vi människor använder siffror överallt i vardagen. Vi kommer i kontakt med det så ofta att vi kan läsa det flytande. Så fort vi ser symbolen “1” kopplar vi det direkt till värdet ett. Kombinationen “23” vet vi betyder “två tior plus tre ettor”.
Vi kanske inte förstår hur stort talet “1 026 245 341 553 566” är, men vi får direkt en uppfattning om det eftersom vi är så bekväma med de regler vårt talsystem har:
Alla talsystem har en bas och symboler som representerar olika värden.
I det decimala talsystemet har vi:
- Basen 10
- Symbolerna 0-9
Men vad betyder det att ha en “bas 10”?
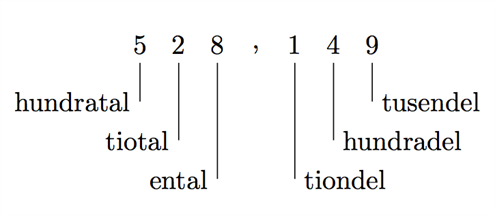
Om vi börjar från entals-positionen (till vänster om kommatecknet), ser vi att för positionen till vänster är värd tio gånger mer, vilket vi kallar för tiotal. Positionen till vänster om tiotalen är värd tio gånger mer än tiotalen, vilket vi kallar för hundratal. Och så vidare. Basen 10 syns i att vi multiplicerar med 10 för varje steg till vänster.
Varför valde vi just det decimala talsystemet, med basen 10?
Troligtvis för att vi har tio fingrar.
Hur ser detta ut rent matematiskt?
I bilden ovan syns hur positionerna är numrerade. Numret representerar exponenten till en bas (den bas vi väljer att jobba i, i vårt fall 10). Värdet av ett tal är detsamma som det sammanlagda värdet av alla koefficienter multiplicerat med basen upphöjt till positionens index.
För att göra detta mer begripligt kan vi ta talet "150,3" som ett exempel.
På position 2 finns symbolen “1”, på position 1 finns “5”, posion 0 ger “0” och på position -1 hittas “3”. Detta betyder att talet har värdet
eller i talspråk,
Om vi redan vet vad 150,3 är varför ska vi göra det komplicerat med koefficienter, exponenter och baser?
Jo, det är nog inte fördelaktigt för oss att dela upp tal i den decimala talbasen för att sedan räkna ihop de igen, men förståelsen för hur tal är uppbyggda är viktigt, för att vi framöver ska kunna “översätta” tal mellan olika talbaser.
För att vara tydlig kan man skriva vilket talsystem man vill att en siffra ska tolkas i. Såhär:
\[ 150{,}3_{10} \]
Nedan följer några exempel på vanliga talsystem:
Unära talsystemet
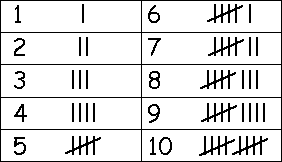
Vi använder det unära talsystemet när vi räknar på fingrarna, eller håller koll på poängen i ett spel. Man brukar också göra ett snedstreck för varje grupp av fem.
Binära talsystemet
| Decimalt | Binärt |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| … | … |
Detta talsystem kommer vi titta närmre på, eftersom det är väldigt viktigt inom digitalteknik. Datorer använder sig av just detta talsystem för att räkna.
Hexadecimala talsystemet
| Decimalt | Hexadecimalt |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| … | … |
| 9 | 9 |
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
| 16 | 10 |
Det hexadecimala talsystemet är på ett sätt ett större talsystem än det decimala, eftersom den har fler symboler, ända från 0 till F (16 stycken). Vi kommer också att titta närmre på detta talsystem, eftersom det är väldigt användbart inom digitalteknik.

